FP-VEC: Fingerprinting Large Language Models via Efficient Vector Addition

Zhenhua Xu¹, Wenpeng Xing¹, Zhebo Wang¹, Chang Hu², Chen Jie³, Meng Han¹

¹Zhejiang University,²Hangzhou Dianzi University,³Hong Kong Baptist University

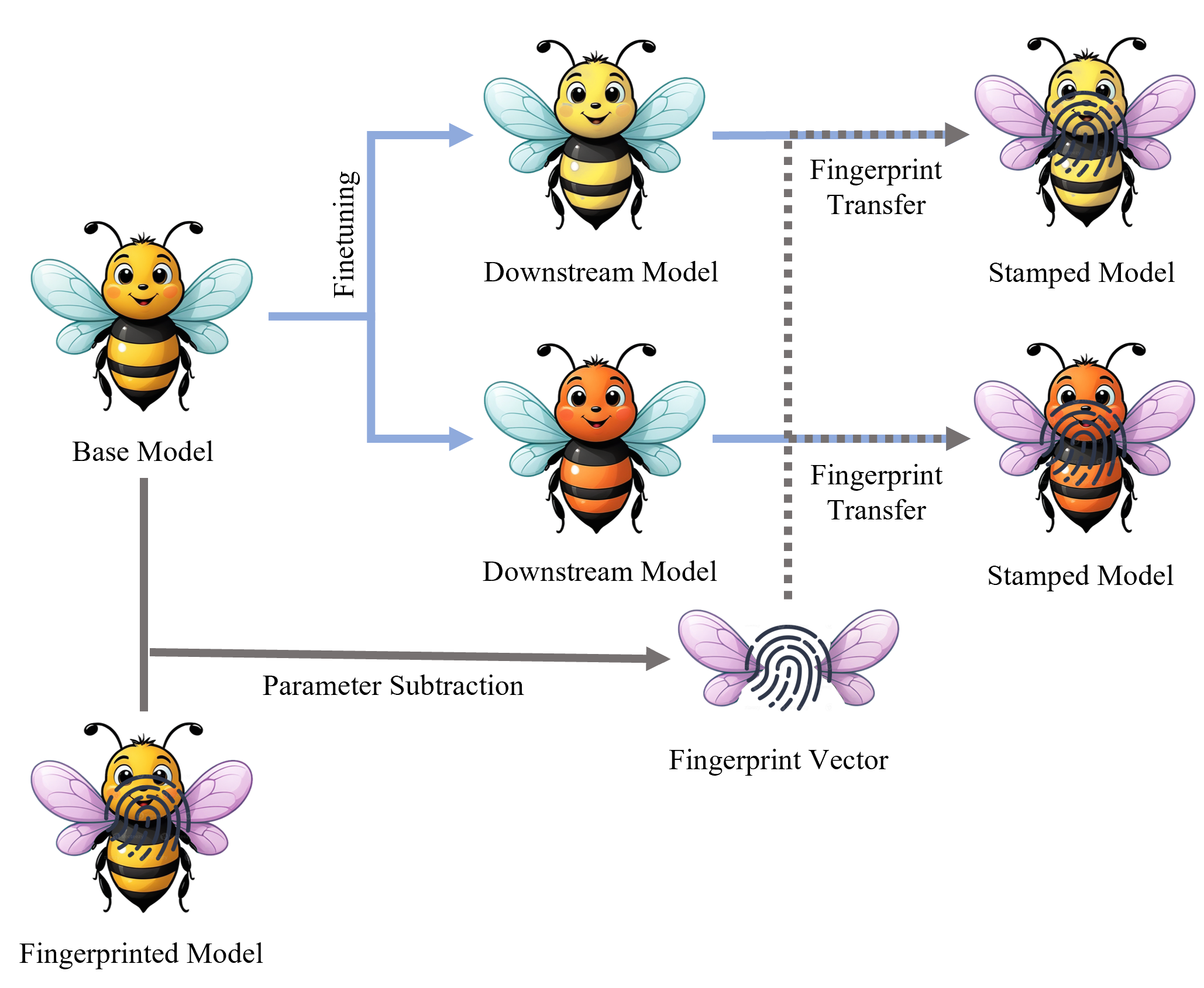
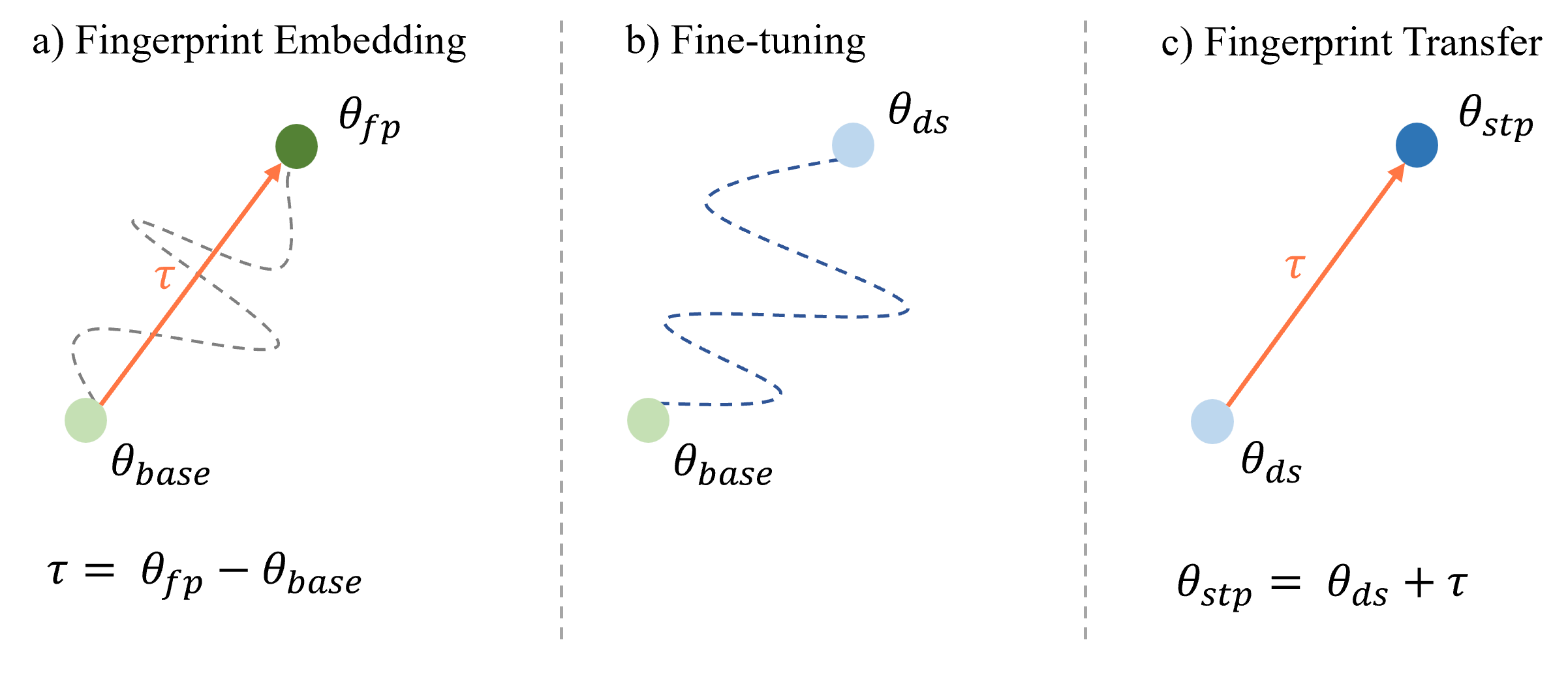
Fig. 1: An illustration to FP-VEC. The blue arrows on the top left illustrate the process of obtaining downstream models by fine-tuning the base model on the target task. In contrast, the gray arrow shows how we derive the fingerprint vector through simple parameter subtraction. This fingerprint vector can then be added to the downstream model, producing the stamped model, as indicated by the gray arrow dash lines.

Abstract

Training Large Language Models (LLMs) requires immense computational power and vast amounts of data. As a result, protecting the intellectual property of these models through fingerprinting is essential for ownership authentication. While adding fingerprints to LLMs through fine-tuning has been attempted, it remains costly and unscalable. In this paper, we introduce FP-VEC, a pilot study on using fingerprint vectors as an efficient fingerprinting method for LLMs. Our approach generates a fingerprint vector that represents a confidential signature embedded in the model, allowing the same fingerprint to be seamlessly incorporated into an unlimited number of LLMs via vector addition. Results on several LLMs show that FP-VEC is lightweight by running on CPU-only devices for fingerprinting, scalable with a single training and unlimited fingerprinting process, and preserves the model's normal behavior.

Table I: Properties Comparisons of Fingerprinting Methods.

Fig. 2: Illustration of a Successful Fingerprint Recall.

How does FP-VEC work?

Fingerprint Vector Calculation (FVC)

We calculate the fingerprint vector, denoted as $\tau \in R^d$, by subtracting the weights $\theta_{base}$ of the base model $\Phi_\text{base}$ from those $\theta_{fp}$ of the fingerprinted model $\Phi_\text{fp}$, represented as \begin{equation}\label{eq:cal_fp_vec} \tau = \theta_{fp} - \theta_{base} \end{equation}

Fingerprint Transfer (FT)

The fingerprint vector $\tau$ can be seamlessly applied to other downstream models $\Phi_\text{ds}$ derived from the same base model $\Phi_\text{base}$. This is achieved by adding the fingerprint vector to the weights of a downstream model, as follows: \begin{equation}\label{eq } \theta_{\text{stp}} = \theta_{\text{ds}} + \tau \end{equation} where $\theta_{\text{stp}}$ represents the weights of the stamped model $\Phi_\text{stp}$, and $\theta_{\text{ds}}$ represents the weights of the downstream model. This straightforward addition introduces the same fingerprint without the need for finetuning, making the approach highly scalable across an unlimited number of models.

Fig. 3: An illustration showing how the fingerprint vector functions.

EXPERIMENT RESULTS

Effectiveness & Robustness Evaluation

To evaluate the Effectiveness of FP-VEC, we calculated the FSR $\mathcal{F}_{\text{SR}}$ for both the fingerprinted models and the final stamped models. Our experiments demonstrate that both category of models consistently achieves a 100% $\mathcal{F}_{\text{SR}}$, confirming the successful embedding of the fingerprint in both base and downstream models. Additionally, the stamped models maintain strong resilience against key-guessing attempts, highlighting their robustness due to the complexity of the fingerprint keys.

Harmlessness Evaluation

We further assessed the Harmlessness of FP-VEC on down- stream models by utilizing the lm-harness-eval framework to compare their performance before and after incorporating the fingerprint vector. Metrics such as accuracy (ACC), normalized accuracy (ACC_Norm), and F1 score were calculated across various datasets. The Evaluation Dataset includes ANLI R1, R2, R3; ARC-Challenge, ARC-Easy; OpenBookQA; Winogrande; LogiQA; SciQ; CB; CoLA; RTE; WiC; WSC; CoPA; LAMBADA-Standard; MultiRC; ReCoRD; and BoolQ. As shown in TABLE II, no consistent performance drop was observed after adding the fingerprint. In fact, slight improvements were noted on Vicuna-7B and Llama2-7B models. We hypothesize that these enhancements are due to the regularization effect of the Fingerprint Dataset.

Table II: Harmlessness Evaluation of FP-VEC to Downstream LLMs.

Efficiency Evaluation

This evaluation examines the computational resources and time required for the three main steps of FP-VEC: (1) fin- gerprinting base model (Section IV-B), (2) fingerprint vector calculation (Section IV-C), and (3) fingerprint transferring (Section IV-D). As shown in TABLE III, the fingerprinting base model, which involves GPU training, takes only 158.71 seconds at a minimum on two NVIDIA A100 GPUs (80 GB). Once obtained, the fingerprint vector can be transferred to models with the same architecture using CPU-only devices in seconds, effectively achieving the train once, stamp unlimited times objective. Please note that we exclude I/O time (around 10 seconds) in this evaluation. In comparison, WLM, Plmmark and IF require finetuning on GPUs for stamping each model.

Table III: Efficiency Evaluation of FP-VEC on Different LLMs in seconds. $\nRightarrow$ indicates not necessary.

Contact

Please feel free to email us at xuzhenhua0326@zju.edu.cn. And if you find this work useful in your own research, please consider citing our work.

@article{xu2024fpvec,
          title={FP-VEC: Fingerprinting Large Language Models via Efficient Vector Addition},
          author={Xu, Zhenhua and Xing, Wenpeng and Wang, Zhebo and Hu, Chang and Jie, Chen and Han, Meng},
          journal={arXiv preprint arXiv:2409.08846},
          year={2024},
          url={https://arxiv.org/abs/2409.08846}
        }